The origin of impossible figures

Before the 20th century

In 1754, William Hogarth, an English painter and engraver, published an etching entitled "False Perspective" in which he shows his contemporary draughtsmen what mistakes in perspective they must not make in their works.

In the 20th century

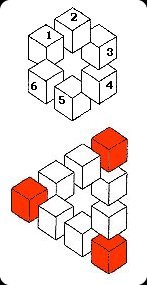The first artist to draw an impossible figure was Oscar Reutersvärd in 1934, and it was through a chance occurrence! After drawing a six-pointed star surrounded by six cubes (numbered from 1 to 6 in the illustration), he added three more cubes (the red ones in the illustration) to form a triangle. That first "paradoxical" figure was followed by more than 2,500 drawings of impossible objects!

A quarter of a century later, in 1958, an English mathematician named Roger Penrose reinvented Reutersvärd's triangle and gave him his name. In that same year, Dutch artist M. C. Escher published his rendering of Necker's cube to general acclaim, thus being the first one to draw an "impossible cube". Escher has left us four works representing impossible objets: "Convex and Concave", "Belvedere", "Ascending and Descending" and "Waterfall".

Impossible objects

One of the most exciting questions about impossible objects is the following: "Do they exist or don't they?" As long as the object is only a drawing, it makes no doubt that it does exist. However, as soon as it leaves the flat piece of paper or canvas to enter the three-dimensional world, it seems indeed impossible for the object to exist in it as it has been drawn. That is why we concern ourselves here with impossible objects and not impossible drawings or figures.

Thus the question becomes: "Can one actually make an impossible object after an impossible figure?" Strictly speaking, the answer is "No!" However, one can make a more or less realistic rendering of it. Up to now, the only two solutions imagined presented major drawbacks, the most important being that the object had to be viewed from a very precise angle to produce its illusionistic effect. There are two monumental sculptures of Reutersvärd's impossible triangle: One in Perth, Australia, is an "open" sculpture; the other one, in Ophoven, Belgium, is "twisted". In each case, only the cognoscenti can see them as triangles; for the uninitiated, they are only abstract art.

Tabary is the only one today who has managed to make three-dimensional casts of impossible figures without these drawbacks; in other words, they can be seen by anyone, even the uninitiated, and they are neither twisted nor open. And not only can they be seen by anyone, but thanks to a subtle play of light and shadow brought about by natural daylight or an artificial source which gives them volume and "reality", they look like works of kinetic art when the observer moves while gazing at them.

Ambigrams

An ambigram (or inversion) is a word which, seen from a certain angle or after being rotated, shows the same word or a different one. It is an exercise in calligraphy in which optical illusions and symmetries play an essential role.

Different types of ambigrams

• Simple ambigrams

  The word remains unchanged after being rotated by 180°.

  Exemples :

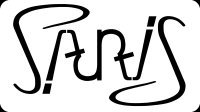
  Paris will always be Paris
  ART stays ART
  LOVE is forever LOVE

• Double ambigrams

  The word changes into another word after being rotated, but both words remain linked by their meanings.

  Here is an example of a 180° central rotation:

  
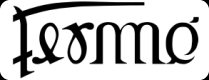
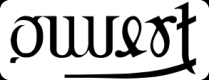
  Fermé / Ouvert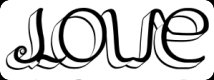
  
  Love / Amor (see sculpture)

  Here is another example, of a 180° vertical rotation:

  Tabary / Francis
   
  Design by Ph. Starck

  This is an example of a 180° horizontal rotation:

  
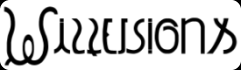
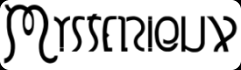
  Les illusions / Mystérieux
  
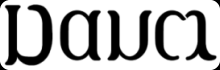
  Nancy / Daum

The creators of ambigrams

The pioneers in this field are Scott Kim and Douglas Hofstadter, but you will find many other creators on the internet.

The uses of ambigrams by Tabary

Ambigrams can be used in advertising, provided an appropriate support can be found for them. Designed as sculptures, they add to them an element of magic and ambivalence.